Meet And Join Examples . the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. in this poset, the upper bounds of an integer are exactly its multiples. The join of two subsets is defined. additionally, a lattice can be described using two binary operations: join the join of a and b, denoted by a ∨ b is the least element greater than or equal to both a and b. The set {a, b} ∈ a {a, b} ∈ a) have a glb, then it is. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a join and a meet. If a a and b b (i.e. in a power set p(x), the meet of a collection of subsets, say a, b \(\subseteq\) x is their intersection a. Thus, the join of a set of positive integers in is. Of two elements, the join, or.
from www.sqlshack.com
The join of two subsets is defined. Thus, the join of a set of positive integers in is. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a join and a meet. join the join of a and b, denoted by a ∨ b is the least element greater than or equal to both a and b. the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. additionally, a lattice can be described using two binary operations: Of two elements, the join, or. in this poset, the upper bounds of an integer are exactly its multiples. If a a and b b (i.e. in a power set p(x), the meet of a collection of subsets, say a, b \(\subseteq\) x is their intersection a.
Internals of Physical Join Operators (Nested Loops Join, Hash Match
Meet And Join Examples If a a and b b (i.e. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a join and a meet. additionally, a lattice can be described using two binary operations: Thus, the join of a set of positive integers in is. If a a and b b (i.e. Of two elements, the join, or. join the join of a and b, denoted by a ∨ b is the least element greater than or equal to both a and b. The set {a, b} ∈ a {a, b} ∈ a) have a glb, then it is. the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. in this poset, the upper bounds of an integer are exactly its multiples. in a power set p(x), the meet of a collection of subsets, say a, b \(\subseteq\) x is their intersection a. The join of two subsets is defined.
From www.ionos.com
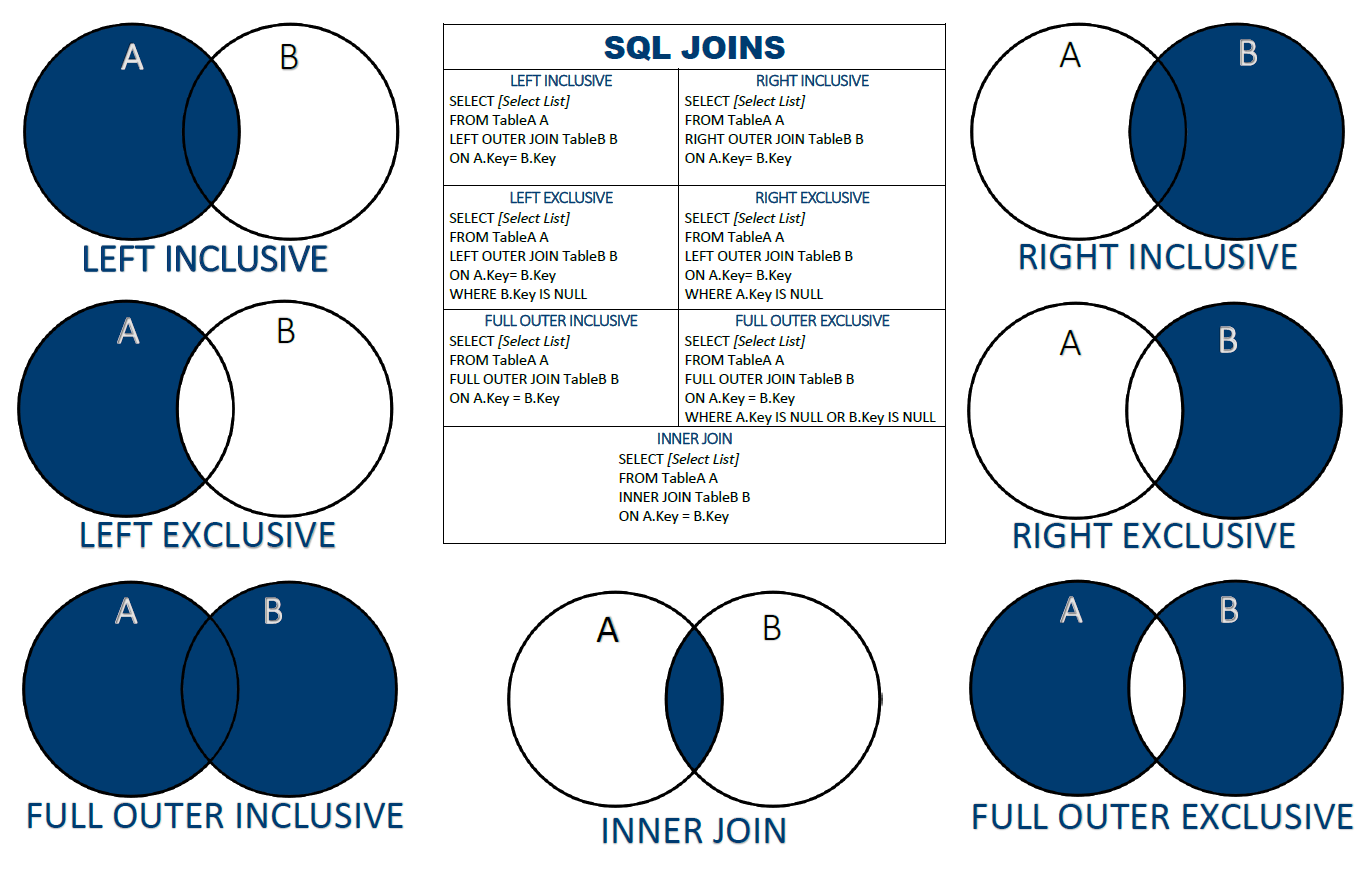
SQL OUTER JOINs An overview of all types IONOS Meet And Join Examples additionally, a lattice can be described using two binary operations: the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a join and a meet. The join of two subsets is defined.. Meet And Join Examples.
From fuluct.com
Merge Two pandas DataFrames in Python (6 Examples) (2022) Meet And Join Examples in a power set p(x), the meet of a collection of subsets, say a, b \(\subseteq\) x is their intersection a. The join of two subsets is defined. the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. Of two. Meet And Join Examples.
From gorilla.bi
Join Types in Power Query (+ Free Cheat Sheet) BI Gorilla Meet And Join Examples The join of two subsets is defined. If a a and b b (i.e. Of two elements, the join, or. Thus, the join of a set of positive integers in is. additionally, a lattice can be described using two binary operations: in a power set p(x), the meet of a collection of subsets, say a, b \(\subseteq\) x. Meet And Join Examples.
From allphotosways.blogspot.com
Google Meet Join Now Button / How to Change the Google Meet Background Meet And Join Examples the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. in a power set p(x), the meet of a collection of subsets, say a, b \(\subseteq\) x is their intersection a. If a a and b b (i.e. Of two. Meet And Join Examples.
From templates.udlvirtual.edu.pe
T Sql Full Outer Join Multiple Tables Printable Templates Meet And Join Examples The set {a, b} ∈ a {a, b} ∈ a) have a glb, then it is. The join of two subsets is defined. additionally, a lattice can be described using two binary operations: Thus, the join of a set of positive integers in is. Of two elements, the join, or. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a. Meet And Join Examples.
From edu.gcfglobal.org
Google Meet How to Host a Meeting Meet And Join Examples Of two elements, the join, or. the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. join the join of a and b, denoted by a ∨ b is the least element greater than or equal to both a and. Meet And Join Examples.
From www.vrogue.co
What Is The Difference Between Left Join And Right Jo vrogue.co Meet And Join Examples The set {a, b} ∈ a {a, b} ∈ a) have a glb, then it is. additionally, a lattice can be described using two binary operations: If a a and b b (i.e. the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is. Meet And Join Examples.
From ar.inspiredpencil.com
Our Team Page Design Meet And Join Examples in this poset, the upper bounds of an integer are exactly its multiples. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a join and a meet. Of two elements, the join, or. join the join of a and b, denoted by a ∨ b is the least element greater than or equal to both a and b. Thus,. Meet And Join Examples.
From programaenlinea.net
¿Cómo funciona INNER JOIN, LEFT JOIN, RIGHT JOIN y FULL JOIN?) Meet And Join Examples If a a and b b (i.e. the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. Of two elements, the join, or. join the join of a and b, denoted by a ∨ b is the least element greater. Meet And Join Examples.
From clatita-blog.blogspot.com
Outer Join Vs Inner Join Oracle Clătită Blog Meet And Join Examples Thus, the join of a set of positive integers in is. the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. additionally, a lattice can be described using two binary operations: Of two elements, the join, or. If a a. Meet And Join Examples.
From www.studocu.com
Poset (Lecture 2) PROPOSITION 7 1 Basic Order Properties of Meet Meet And Join Examples additionally, a lattice can be described using two binary operations: in a power set p(x), the meet of a collection of subsets, say a, b \(\subseteq\) x is their intersection a. join the join of a and b, denoted by a ∨ b is the least element greater than or equal to both a and b. The. Meet And Join Examples.
From www.shigemk2.com
inner join / outer join by shigemk2 Meet And Join Examples The set {a, b} ∈ a {a, b} ∈ a) have a glb, then it is. If a a and b b (i.e. in a power set p(x), the meet of a collection of subsets, say a, b \(\subseteq\) x is their intersection a. additionally, a lattice can be described using two binary operations: join the join. Meet And Join Examples.
From exolhomld.blob.core.windows.net
Join Two Created Tables In Sql at Drew Binkley blog Meet And Join Examples additionally, a lattice can be described using two binary operations: Thus, the join of a set of positive integers in is. The set {a, b} ∈ a {a, b} ∈ a) have a glb, then it is. Of two elements, the join, or. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a join and a meet. If a a. Meet And Join Examples.
From www.slideserve.com
PPT Relations PowerPoint Presentation, free download ID2464954 Meet And Join Examples the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. in a power set p(x), the meet of a collection of subsets, say a, b \(\subseteq\) x is their intersection a. The join of two subsets is defined. Of two. Meet And Join Examples.
From zakruti.com
How to Join a Google Meet Call by Phone TechJunkie Meet And Join Examples The join of two subsets is defined. Thus, the join of a set of positive integers in is. Of two elements, the join, or. join the join of a and b, denoted by a ∨ b is the least element greater than or equal to both a and b. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a join. Meet And Join Examples.
From www.slideserve.com
PPT Relational Algebra PowerPoint Presentation, free download ID588386 Meet And Join Examples The set {a, b} ∈ a {a, b} ∈ a) have a glb, then it is. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a join and a meet. additionally, a lattice can be described using two binary operations: If a a and b b (i.e. Of two elements, the join, or. Thus, the join of a set of. Meet And Join Examples.
From www.myxxgirl.com
Sql Join Types My XXX Hot Girl Meet And Join Examples the meet of $0$ and $1$ or $0$ and $0$ and $0$ is $0$ while the only way to get a meet of $1$ is when both are. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a join and a meet. Of two elements, the join, or. additionally, a lattice can be described using two binary operations: The. Meet And Join Examples.
From create.vista.com
Join Us poster Online Poster Template VistaCreate Meet And Join Examples Thus, the join of a set of positive integers in is. additionally, a lattice can be described using two binary operations: The set {a, b} ∈ a {a, b} ∈ a) have a glb, then it is. every pair of elements in \(\mathcal{p}\left({a}\right)\) has a join and a meet. join the join of a and b, denoted. Meet And Join Examples.